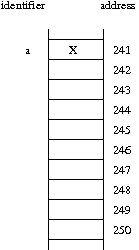
Draw a diagram such as the one shown below, to portray the underlying memory configuration that might exist after the completion of the following series of commands (you may assume that one cell of memory is sufficient for storing a character or a pointer).
char a = 'X';
char b = 'Y';
char *c = &b;
char d(a);
char &e(a);
char *f = c;
char *g = new char('Z');
Based upon your solution in the first diagram, give a second diagram that portrays the updated configuration after the following additional commands.
*f = 'W';
c = g;
e = b;
Assume that we have an initially empty stack, S, of integers. Fill in the following table (we have completed the first two rows), showing the output returned by each method call and the internal state of the stack after that point in time.
| Operation | Output | S (bottom, ..., top) |
| S.push(7) | - | (7) |
| S.push(10) | - | (7, 10) |
| S.pop() | ||
| S.top() | ||
| S.push(3) | ||
| S.push(5) | ||
| S.pop() | ||
| S.empty() | ||
| S.size() | ||
| S.top() | ||
| S.push(8) | ||
| S.pop() | ||
| S.pop() |
Assume that we have an initially empty queue, Q, of integers. Fill in the following table (we have completed the first two rows), showing the output returned by each method call and the internal state of the queue after that point in time.
| Operation |
Output |
Q (front, ..., back) |
| Q.push(10) | - | (10) |
| Q.push(4) | - | (10, 4) |
| Q.size() | ||
| Q.front() | ||
| Q.push(6) | ||
| Q.pop() | ||
| Q.push(3) | ||
| Q.pop() | ||
| Q.front() | ||
| Q.pop() | ||
| Q.push(7) | ||
| Q.front() |
Chapter 4.5.3 of our book discusses the Adapter Design Pattern, which is a technique by which an existing data structure can be retooled to provide an implementation of another abstraction. That example is based on using a double-ended queue (we'll see this soon) to provide the simpler abstractions of a stack and a queue. For this problem, we want you to show how to implement a queue class using nothing other than two stack instances.
Rather than using our own version of the stack and queue, you should assume that we are using the STL version of a stack. This means that you can presume it has infinite capacity. However, it also means that you cannot make any assumptions about the private representation of the stacks (that is, you cannot access the underlying array). You must use the stacks as tools based only on their public behaviors.
For concreteness, we ask that you model your answer to this problem in C++ syntax, using the following framework as the basis.
#include <stack>
template <typename Object>
class queue {
private:
// Do not use any data members other than the following two stacks
std::stack<Object> S1;
std::stack<Object> S2;
public:
bool empty() const {
}
int size() const {
}
void push(const Object& item) {
}
void pop() {
}
Object& front() {
}
// for simplicity, we'll ignore the const version of front()
}; // end of class queue
To give you a flavor of the style of code, a natural implementation for the queue.empty() methiod in this setting might be:
bool empty() const {
return (S1.empty() && S2.empty());
}
since we presume that all elements of the queue must be stored,
and S1 and S2 are your only means of storage.
If you understand the goal, it is now time to think about how to solve the problem. To be successfully, you will need to keep straight your role as the implementor of a queue, yet also your role as a client for the stack. That is, your new structure should behave with the first-in-first-out semantics of a queue. Make sure your code works for any sequence of push(), pop(), and front() operations.
Note: if you prefer a hands-on experience, type up your solution and compile and test it. You could even write a test program that executes the commands from problem B on your queue. But you need only to submit a hardcopy of your solution.