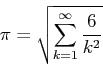Computer Science 1060
Scientific Programming
Assignment 02 - Vectorized Operations

Contents:

Overview

Topic: Vectorized Operations
Related Reading: Ch. 3 as well as coverage of vectors from lecture as well as the practice problems that we did in class.

For this assignment, you should be submitting four separate files: approxPi.m, limits.m, baseball.m, floatingError.m.
Submit your m-files via email to dferry_submit@slu.edu.

Problems to be Submitted (20 points)

Problem A)

The value of $\pi$ can be estimated by evaluating a partial sum of the form

\begin{displaymath}\pi = 4 \left(\frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \ldots\right)\end{displaymath}

Write a script named approxPi.m which computes the first million terms of this series. Then use cumsum to compute the partial sums (as was done in the sample solutions from lecture). As a final result, store the relative error between MATLAB's pi and our approximate pi for the values $N = 10, 100, 1000, 10000, 100000, 1000000$ in a vector called errorsPi.

Problem B)
Through calculus, it is possible to show that

\begin{displaymath}\lim_{x \rightarrow 0} \frac{e^x -1}{x} = 1.\end{displaymath}

For this problem, we want you to gather empirical evidence for that limit by evaluating the expression for progressively smaller values. Specifically, write a script named limits.m that creates a vector called limit by evaluating the expression for values of $x$ in the series $1, \frac{1}{2}, \frac{1}{4}, \ldots, \frac{1}{2^{25}}$. Display your results by executing the following commands: 

format long;
disp(data');disp(limit');

Problem C)

For this problem, we consider the motion of a ball under the force of gravity (we will ignore other factors such as air resistance). Let $g = 9.8$ is the acceleration due to gravity, measured in $m/s^2$. If a ball is thrown vertically with an initial velocity of $v_0$, measured in meters/second), it will remain in the air for $\frac{2v_0}{g}$ seconds. Its height at time $t$ measured in meters will be

\begin{displaymath}h_t = v_0 \cdot t - \frac{g \cdot t^2}{2}\end{displaymath}

Write a script baseball.m that creates a vector named time with 25 evenly spaced values from $0$ to $\frac{2v_0}{g}$. Then compute another vector named height that tracks the corresponding height for each time, using the above formula.

Test your program using an initial velocity of 43.81 meters/second (the equivalent of a 98 m.p.h. fastball). To produce a two-column display of your results, use the command disp( [time', height'] );

Lastly, use the max function to find the maximum value of your height vector, and store this in a variable called maxHeight

Problem D)

For any non-zero real number, we have the identity that $ x \cdot \frac{1}{x} = 1$. However, computers do not perform arithmetic with arbitrary precision. Instead, they use a convention known as floating-point representation for storing and manipulating numbers with fixed precision. We can find evidence of this by trying to verify the above mathematical identity. If you perform the test 3 * (1 / 3) == 1, you will likely see that the equivalence is true (with the logical true value displayed as ``1'' in matlab). Yet if you perform the similar test 49 * (1 / 49) == 1, the condition is false (with the logical false value displayed as ``0'' in matlab).

Write a script named floatingError.m that performs the following experiment. Determine what percentage of the first 100000 integers successfully satisfy the identity $ x \cdot \frac{1}{x} = 1$ when computed in MATLAB. Count how many integers satisfy the identity in a variable called numCorrect, and store the percentage of correct integers in a variable called correctRate.

Extra Credit (2 points)
Problem E)
Mathematicians have developed several expressions for computing the value of $\pi$ based on infinite series. We saw one in the first problem. Here are two additional forms:

\begin{displaymath}\pi = \sqrt{\sum_{k=1}^{\infty} \frac{6}{k^2}}\end{displaymath}


\begin{displaymath}\pi = \sqrt{8 + \sum_{k=1}^{\infty} \frac{16}{(2k-1)^2 \cdot (2k+1)^2}}\end{displaymath}

Write a script named extra.m which repeats the exercise from Problem A using each of the new approaches. Compare the relative errors of the three approximations for varying values of $N$.

Originally by:
Michael Goldwasser