cos423: Theory of Algorithms	handout #21
Michael Goldwasser
Princeton University	Tuesday, April 14, 1998

Homework #8:	Classes P vs. NP, Reductions
Due Date:	Tuesday, April 21, 1998 (5:00pm)

Collaboration Policy

You may collaborate with others on this entire homework. However, please re-read the policy guidelines from Handout #1.

Reading

Read Chapter 36 of CLR, although you may gloss over the parts on the circuit satisfiability problem, including the book's version of the Cook-Levin theorem on pages 933-938.

Practice

Recall, these exercises are purely for your own practice. You need only turn in the official problems.

Do CLR 36.1-1.
Do CLR 36.3-1.
Do CLR 36.4-4.
Do CLR 36.5-1.

Problems

1.

(30 points) Show that if HAM-CYCLE $\in$ P, then the problem of listing the vertices of a Hamiltonian cycle, in order, is polynomial-time solvable. More specifically, assume that there exists a polynomial-time procedure TEST-HAM-CYCLE(G'), which takes any graph G' and returns True/False depending on whether or not G' has a Hamiltonian cycle or not. We want you to design a procedure PRINT-HAM-CYCLE(G) which will actually print the order of a legitimate Hamiltonian cycle of G, assuming one exists. Of course, your algorithm is allowed to call TEST-HAM-CYCLE as needed. Please give high-level pseudo-code for your new procedure, and argue (briefly) why your algorithm is correct, and why it runs in polynomial time.

2.

(30 points) The set-partition problem takes as input a set S of numbers. The question is whether the numbers can be partitioned into two sets A and $\overline{A} = S-A$ , such that $\sum_{x \in A} = \sum_{x \in \overline{A}}$ . Show that the set-partition problem is NP-Complete. (Hint: looks a bit like Subset-Sum, doesn't it?!)

3.

(40 points) A k-coloring of an undirected graph G = (V,E) is a function $c: V \leftarrow \{1,2,\ldots,k\}$ such that $c(u) \neq c(v)$ for every edge $(u,v) \in E$ . In other words, the numbers $1,2,\ldots,k$ represent the k colors, and adjacent vertices must have different colors. We define the k-COLOR problem to decide whether or not a given graph can be colored using k colors.

Prove that 2-COLOR $\in$ P.
Prove that 3-COLOR $\in$ NP.

To prove that 3-COLOR is NP-Hard (and thus NP-Complete by part 3b), we use a reduction from 3-CNF-SAT. Given a formula $\phi$ of m clauses on n variables $x_1, x_2, \ldots, x_n$ , we construct a graph G = (V,E) as follows. To start with, we create a vertex for each variable, a vertex for the negation of each variable, and three special vertices: true, false, red. We add edges to form a triangle on the three special vertices, and we also add a triangle on $x_i, \neg x_i$ , and red for each $i=1,2,\ldots,n$ . Now, for each clause $(p \vee q \vee r)$ , we create a widget, as shown in the figure below, where the five black vertices are newly created for each separate clause, but the other four vertices are among those we have already introduced.

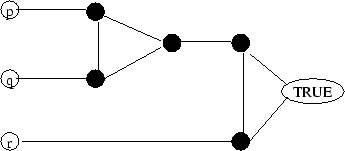
$\psfig {figure=hw08.figures/widget.eps,width=3in}$

Argue that for our graph G to be 3-colorable, it must be that 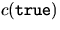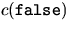$c({\tt true })$ , $c({\tt false})$ and $c({\tt red})$ use three distinct colors.
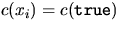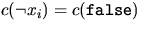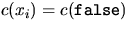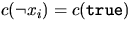Argue that for our graph G to be 3-colorable, it must either be the case that $c(x_i) = c({\tt true})$ and $c(\neg x_i) = c({\tt false})$ or else that $c(x_i) = c({\tt false})$ and $c(\neg x_i) = c({\tt true})$ for a given variable x_i.
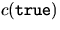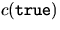Argue that for our graph G to be 3-colorable, it must be that one of c(p), c(q), c(r) is equal to $c({\tt true })$ , for a given widget. Conversely, argue that so long as any one of c(p), c(q), c(r) is equal to $c({\tt true })$ , then that particular widget can be successfully 3-colored (at least, locally).
Prove that if graph G is 3-colorable, then 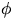$\phi$ is satisfiable.
Prove that if graph G is not 3-colorable, then 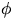$\phi$ is not satisfiable.
Complete the overall proof that 3-CNF-SAT 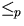$\leq_p$ 3-COLOR, and thus that 3-COLOR is NP-Hard.

Extra Credit

Let the Set-Splitting problem be defined as follows. The input is a finite set S, and a collection of subsets $C_1, C_2, \ldots, C_k$ of the set S. An algorithm should return true if it is possible to color the elements of S red or blue in a way so that no C_i has all its elements colored with the same color.

Show that Set-Splitting is NP-Complete. (sorry, no hints on the extra credit problem)

This document was generated using the LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)