Contents:

• Overview
• Internet Requirements
• Practice Problems
• Problems to be Submitted
• Extra Credit

Topic: High-Level Programming in Python
Related Reading: Ch. 8.1-8.3 of Dale/Lewis, as well as lecture notes on Python
Due: 8pm Thursday, 21 October 2004

For this assignment, we will rely heavily on the Python environment demonstrated in class. You will need to have an Internet connection to run this software.

1. Exercise 53 of Ch. 8 (p. 279); answer in back of text

2. Exercise 68 of Ch. 8 (p. 281)

3. Exercise 70 of Ch. 8 (p. 281)

4. Exercise 75 of Ch. 8 (p. 281); answer in back of text

5. In the lecture notes, we demonstrate a program to print all odd numbers from 1 to 20. That approach was based on a loop which counts from 1 to 20, and then a conditional statement nested in the loop body to filter odd vs. even numbers.

   Another approach to accomplish the same result is by using a loop which counts from 1 to 10, with the body of the loop printing out the k^th odd number, which has the form 2*k-1.

   Use this new approach to write Python code for printing out the first ten odd numbers. (solution available online)

6. Review all of the code fragments in our Python lecture notes

1. (4 points)

   Determine whether the following Boolean expressions are true of false

   1. 7 < 7
   2. 8 >= 8
   3. (5 > 3) or (6 < 2)
   4. ((7 > 3) or (4 > 6)) and (6 < 2)

2. (4 points)

   For this problem, you can use python to do the work for you if you'd like. Though on a test, you would certainly be expected to do such a problem on your own, so please make sure that you fully understand the answer.

   1. What value or sequence of values would be printed when running the following segment of code?

      val = 3
      while val<6:
        print val
        val = val + 1	    
      

   2. What value or sequence of values would be printed when running the following segment of code?

      val = 11
      while val>=7:
        val = val - 1	    
        print val
      

3. (4 points)

   The lecture notes on Python describe how to use nested loops to create textual output diagraming the lower-left triangle of a square.

   For this problem, develop Python code which produces the following diagram:

                     *
                   * *
                 * * *
               * * * *
             * * * * *
           * * * * * *
         * * * * * * *
       * * * * * * * *
     * * * * * * * * *
   * * * * * * * * * *
   

4. (4 points)

   We can define an alternating, mathematical sequence, based upon terms defined as follows, for k>=1,

   

   where the term is positive when k is odd, and negative when k is even. (though this definition may seem arbitrary, the extra credit problem will demonstrate the significance).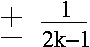

   Before going on, let's doublecheck the definition on some preliminary values of k:

   k	term(k)
   1	+1/1 = 1.0
   2	-1/3 = -0.33333
   3	+1/5 = 0.2
   4	-1/7 = -0.142857

   For this problem we wish to have you write a python program which does the following:

   • Defines a subprogram, term(k) which takes a parameter k and returns the proper value for the k^th term.

   • Then, demonstrates the use of that program by executing a loop which prints out the values of the terms as k ranges from 1 to 10.

   Advice: In calculating the fraction, you need to force the use of floating point numbers. That is 1/5 is evaluated as 0 if division is integral. But 1.0/5.0 results in 0.2 as the data is represented using floating point precision. In fact, 1.0/5 results in 0.2, because once one of the two operands is represented as a floating point number, then the floating point version of division will be used.

5. (4 points)

   At the end of Ch. 8 there are a series of "Thought Questions" (pp. 282-283). Choose any one of those questions to answer. The length of your answer should be appropriate for the question, however I envision answers in the range of 1/2-page to 1-page.

6. (2 points)

   There is an interesting way to approximate the value of PI follows. The value of π turns out to be precisely equal to the following (infinite) series: π = 4*(1/1 - 1/3 + 1/5 - 1/7 + 1/9 - ...).

   Of course, we don't have the time to evaluate an infinite series, so we cannot calculate the exact value for π. But we can get a very good approximation by computing the first n terms of the above series for a given integer n. The more terms we consider, the more accurate our results.

   Write Python code which inputs a natural number n, and outputs the approximation for π based upon the first n terms of the above series.

   Our Advice

   • This is a big task. Don't just start typing, but think about how to break the task up into reasonable pieces. We have already seen how a subprogram can be used to calculate the k^th term. We suggest the following flow of control for the extra credit task:

     • Keep a running sum, initially zero.
     • Design a loop based on a count from 1 to N
     • Within the loop body, add the newest term to the sum.
     • After the loop output the final result (make sure to multiply by 4, if you had not distributed that term into the series)

   • As a test, here are some sample results

     value of n	resulting approximation
     5	3.3396825396825403
     100	3.1315929035585537
     1000	3.140592653839794
     1000	3.140592653839794
     10000	3.1414926535900345
     100000	3.1415826535897198
     1000000	3.1415916535897743
     10000000	3.1415925535897915

     (though admittedly it starts to take a while to do the calculation as n increases)