Contents:

This assignment will use the Rosetta software from the Decker/Hirshfield text. The practice problems will include an introduction to using the software. Also, please see the following information regarding using the Decker/Hirschfield software.

Warning: For larger expressions and longer programs, the software scrolls down as needed. There are scrollbars in the windows which appear to imply that the user is able to scroll back up to the top, however it seems that these scrollbars do not work properly. Just keep this in mind if you play with larger examples.

1. (8 points)
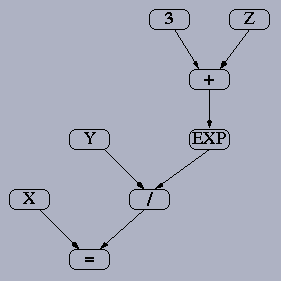
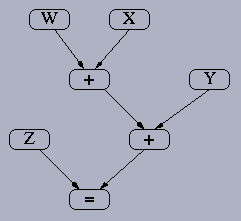
   See if you can match parse trees with their corresponding statements. For each of the parse trees below, write the statement that it represents. You may choose to use Rosetta to confirm your answers if you wish (though you do NOT need to submit your Rosetta work).
   1. 
   2. 
   3. 

2. (8 points)
   For each of the PIPPIN code segments below, find an arithmetic statement that corresponds to it. You may choose to use Rosetta to confirm your answers if you wish (though you do NOT need to submit your Rosetta work).

   1. LOD #3
      MUL Y
      ADD X
      STO W
      

   2. LOD X
      DIV Y
      STO T1
      LOD #3
      SUB T1
      STO Z
      

   3. LOD #2
      MUL Y
      STO T1
      LOD Z
      DIV #3
      STO T2
      LOD T1
      SUB T2
      STO X
      

3. (4 points)
   The goal of this problem is to give you some experience in being a software tester. Someone has written a program intended to build parse trees for evaluating general arithmetic expressions. This software does not allow variables in expression, only positive integers.

   The intended "grammer" which defines the syntax of a valid expression can be shown, in the style of the Brookshear text through the following syntax diagram.
   

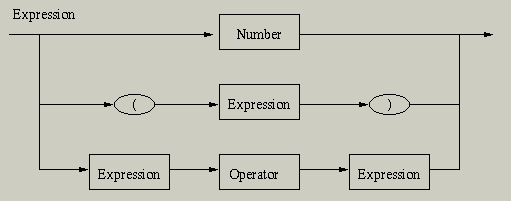
   To avoid ambiguity, the semantics of an expression is interpretted using the standard rules of operator precedence, as discussed in lecture.

   Unfortunately, the software is flawed. Your goal is to identify a well-formed arithmetic expression, according to the above grammer, for which the provided software behaves improperly. To accomplish this testing, you will need to make sure that you understand understand the syntax of the grammer and the semantics of the operator precedence (otherwise, how will you know to recognize incorrect behaviors).

   Please note: If the program reports "Expression not well-formed" this means that the expression you typed is flawed, not the program.

   In your solutions, you are to provide the following information:

   An example of a well-formed arithmetic expression.
   The value which the software errantly reports when evaluating the above expression.
   The value which should have been reported by a correct program.
   
   If you understand your goal, click here to run the proposed software.

   ---

   Overall, please type your answers to all problems to be submitted in a single text document to be submitted.

   ---

   Extra Credit (up to 3 points)

   Code Optimization: The primary goal of a compiler is to take a program in a high-level language, and convert it to a correct machine language program. A secondary goal, however, is to try to produce the most efficient machine code possible. That is, two different machine language programs may solve the same task, but one may do so with fewer overall instructions, or use fewer memory locations for temporary storage.

   For example, if you look carefully at Rosetta's code generation, you will notice that it generally uses memory locations W,X,Y,Z to signify the original inputs and the final results. It uses 'registers' T1, T2, T3, T4 at times to temporarily store a partial computation.

   For extra credit, we are going to examine code for the expression:

   W = (X/3) - ( (Y-3) / (Z+2) )
   

   If you type this expression into Rosetta and allow it to generate code, you will notice that the code makes use of three extra registers at various times: T1, T2, T3. This is somewhat wasteful. With care, it is possible to design PIPPIN code for evaluating this expression which only uses one such register. This can be done by carefully restructuring the order of various computations along the way.

   For extra credit, try to write your own PIPPIN code for evaluating the given expression using as few registers as possible. We will give you three points if your solution uses only one register! If you find a solution which uses only two registers (rather than the original three), we will give you 1 of the 3 possible points.

   Save your PIPPIN code in a file named "Optimized" to be submitted.

   Note: code optimization is only useful if you are still producing code which produces the correct final result. No points will be given for code which does not correctly evaluate the original expression.

   ---

   comp150 Class Page
   mhg@cs.luc.edu
   Last modified: 20 February 2002

   ---