cos423: Theory of Algorithms	handout #2
Michael Goldwasser
Princeton University	Tuesday, February 3, 1998

Homework #1:	Asymptotics and algorithm analysis
Due Date:	Tuesday, February 10, 1998 (9:00am)

Reading

Read carefully Ch. 1, Ch. 2, Ch. 4.1-4.3, and Ch. 18 of CLR.

Practice

Recall, these exercises are purely for your own practice. You need only turn in the official problems.

Do CLR 2.1-1, 2.1-2.
Do CLR 2.1-4.
Do CLR 2.1-6.
Do CLR 2.2-4. [can you do this without Stirling's approximation?]
Do CLR 2.2-5, 2.2-6.
Do CLR 4-1. [Make sure you are familiar with this problem!]

Collaboration Policy

Work entirely on your own for all of these problems.

Problems

1.

(CLR 2-3a). Rank the following functions by order of growth, i.e., find an arrangement $g_1, g_2, \ldots, g_{30}$ of the functions satisfying $g_1=\Omega(g_2), g_2=\Omega(g_3), \ldots, \break g_{29}=\Omega(g_{30})$ . Partition your list into equivalence classes such that f(n) and g(n) are in the same class iff $f(n)=\Theta(g(n))$ .

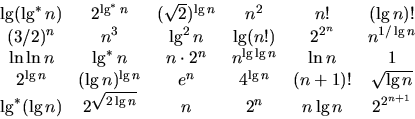
$\begin{displaymath} \begin{array} {cccccc} \lg(\lg^*n) & 2^{\lg^* n} & (\sqrt{2}... ...& 2^{\sqrt{2\lg n}} & n & 2^n & n\lg n & 2^{2^{n+1}}\end{array}\end{displaymath}$

[Note: We do not require formal proof for this problem, simply the ordering and the equivalence classes.]

2.

(CLR 2-4)

Let f(n) and g(n) be asymptotically positive functions. Prove or disprove each of the following conjectures.

f(n) = O(g(n)) implies g(n) = O(f(n)).
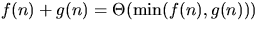$f(n) + g(n) = \Theta(\min(f(n),g(n)))$ .
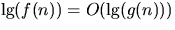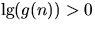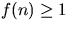f(n) = O(g(n)) implies $\lg(f(n)) = O(\lg(g(n)))$ , where $\lg(g(n))\gt$ and $f(n) \geq 1$ for all sufficiently large n.
f(n) = O(g(n)) implies 2^f(n) = O(2^g(n)).
f(n) = O((f(n))²).
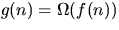f(n) = O(g(n)) implies $g(n) = \Omega(f(n))$ .
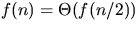$f(n) = \Theta(f(n/2))$ .
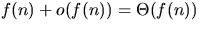$f(n) + o(f(n)) = \Theta(f(n))$ .

[Your proofs must be formal, although for false conjectures a specific counterexample would constitute a valid proof.]

3.

(CLR 18-3)

Amortized weight-balanced trees

Consider an ordinary binary search tree augmented by adding to each node x the field size[x] giving the number of keys stored in the subtree rooted at x. Let $\alpha$ be a constant in the range $1/2 \leq \alpha < 1$ . We say that a given node x is $\alpha$ -balanced if

$size[left[x]] \leq \alpha \cdot size[x]$

and

$size[right[x]] \leq \alpha \cdot size[x]$ .

The tree as a whole is $\alpha$ -balanced if every node in the tree is $\alpha$ -balanced. The following amortized approach to maintaining weight-balanced trees was suggested by G. Varghese.

A 1/2-balanced tree is, in a sense, as balanced as it can be. Given a node x in an arbitrary binary search tree, show how to rebuild the subtree rooted at x so that it becomes 1/2-balanced. Your algorithm should run in time $\Theta(size[x])$ , and it can use O(size[x]) auxiliary storage.
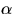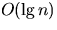Show that performing a search in an n-node $\alpha$ -balanced binary search tree takes $O(\lg n)$ worst-case time.

For the remainder of this problem, assume that the constant $\alpha$ is strictly greater than 1/2. Suppose that Insert and Delete are implemented as usual for an n-node binary search tree, except that after every such operation, if any node in the tree is no longer $\alpha$ -balanced, then the subtree rotted at the highest such node in the tree is ``rebuilt'' so that it becomes 1/2-balanced.

We shall analyze this rebuilding scheme using the potential method. For a node x in a binary search tree T, we define

$\begin{displaymath} \Delta(x) = \vert size[left[x]] - size[right[x]]\vert\mbox{,}\end{displaymath}$

and we define the potential of T as

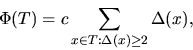
$\begin{displaymath} \Phi(T) = c \sum_{x \in T: \Delta(x) \geq 2} \Delta(x),\end{displaymath}$

where c is a sufficiently large constant that depends on $\alpha$ .

Argue that any binary search tree has nonnegative potential and that a 1/2-balanced tree has potential 0.
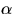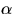Suppose that m units of potential can pay for rebuilding an m-node subtree. How large must c be in terms of $\alpha$ in order for it to take O(1) amortized time to rebuild a subtree that is not $\alpha$ -balanced?
Show that inserting a node into or deleting a node from an n-node 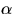$\alpha$ -balanced tree costs 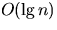$O(\lg n)$ amortized time.

Extra Credit

Finding the missing integer (CLR 4-2)

An array A[1..n] contains all the integers from to n except one. It would be easy to determine the missing integer in O(n) time by using an auxiliary array B[0..n] to record which numbers appear in A. In this problem, however, we cannot access an entire integer in A with a single operation. The elements of A are represented in binary, and the only operation we can use to access them is ``fetch the jth bit of A[i],'' which takes constant time.

Show that if we use only this operation, we can still determine the missing integer in O(n) time.

[To make the analysis cleaner, we will charge your algorithm only for the number of ``bit-fetch'' operations. The input to the algorithm consists of an array of n numbers, each of which is comprised of $\ceil{\lg n}$ bits. Give an algorithm which can find the missing number by fetching only O(n) bits.]

This document was generated using the LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)