| Homework #2: |
Sorting and Selection |
| Due Date: |
Tuesday, February 17, 1998 (9:00am) |
Read Ch. 9.1, Ch. 10.1, and Ch. 10.3 of CLR.
There is a somewhat confusing numbering system for problems from the
textbook. The book has what it terms ``exercises'' which are at the
end of each section, and ``problems'' which are at the very end of
each chapter. For example, Exercise 9.1-1 is at the end of Section
9.1 on page 174, whereas Problem 9-1 is at the end of Chapter 9, on
page 183.
Recall, these exercises are purely for your own practice. You need
only turn in the official problems.
- Ex. 9.1-1, 9.1-3 of CLR
- Ex. 10.3-1 of CLR
- Ex. 10.3-7 of CLR
You may collaborate with others on this entire homework.
However, please re-read the policy guidelines from
Handout #1.
- 1.
- CLR 9-1(a-e), (40 points)
In this problem, we prove an 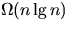 lower bound on the
expected running time of any deterministic comparison sort on n
inputs. We begin by examining a deterministic comparison sort A
with decision tree TA. We assume that every permutation of A's
inputs is equally likely.
lower bound on the
expected running time of any deterministic comparison sort on n
inputs. We begin by examining a deterministic comparison sort A
with decision tree TA. We assume that every permutation of A's
inputs is equally likely.
- 2.
- CLR 9.1-5, (20 points)
Prove that 2n-1 comparisons are necessary in the worst case to merge
two sorted lists containing n elements each. (Note: Make sure
your proof is completely general. That is, you cannot simply argue
that a particular algorithm you have in mind, might take 2n-1
comparisons.)
- 3.
- similar to CLR 10.1-1, (20 points)
Show that the second largest of n elements can be found with
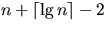 comparisons in the worst case. (
Hint: if you instead find the largest, can you then identify a
subset of elements which must then contain the second largest
item? How large is this subset?)
comparisons in the worst case. (
Hint: if you instead find the largest, can you then identify a
subset of elements which must then contain the second largest
item? How large is this subset?)
- 4.
- CLR 10.3-8, (20 points)
Let X[1..n] and Y[1..n] be two arrays, each containing n
numbers already in sorted order. Give an 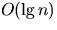 -time algorithm
to find the median of all 2n elements in arrays X and Y. (
Hint: If X[k] is the median of array X, how quickly can you
determine whether it is also the median of the combined 2n elements?
If it is not, did you learn any new information about the identity of
the true median?)
-time algorithm
to find the median of all 2n elements in arrays X and Y. (
Hint: If X[k] is the median of array X, how quickly can you
determine whether it is also the median of the combined 2n elements?
If it is not, did you learn any new information about the identity of
the true median?)
We want to show that the upper bound in Problem 3
was the best possible result. Give an adversarial argument that
any algorithm will require 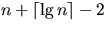 comparisons
in the worst case. (Hint: Argue that in the process of finding
the second largest element, any algorithm must have also determined
the largest element. Now consider the set of elements which lost a
comparison to the largest element. How can an adversary try to make
this set as large as possible? How does this translate into a lower
bound for finding the second largest element?)
comparisons
in the worst case. (Hint: Argue that in the process of finding
the second largest element, any algorithm must have also determined
the largest element. Now consider the set of elements which lost a
comparison to the largest element. How can an adversary try to make
this set as large as possible? How does this translate into a lower
bound for finding the second largest element?)
This document was generated using the
LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
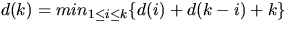 . (Hint: Consider a tree T with k leaves that
achieves the minimum. Let i be the number of leaves in RT and
k-i the number of leaves in LT.)
. (Hint: Consider a tree T with k leaves that
achieves the minimum. Let i be the number of leaves in RT and
k-i the number of leaves in LT.)
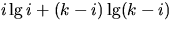 is minimized at i=k/2. Conclude that
is minimized at i=k/2. Conclude that 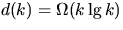 .
.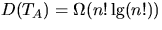 for TA, and
conclude that the expected time to sort n elements is
for TA, and
conclude that the expected time to sort n elements is 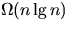 .
.