| Homework #5: |
Randomized Algorithms |
| Due Date: |
Tuesday, March 31, 1998 (5:00pm) |
For the first half of the course, homeworks were due at 9:00 a.m. on
the due date, and late homeworks were accepted up until 5:00 p.m. that
same day, with a penalty.
For the second half of the course, we will accept homeworks up until
5:00 p.m. with no penalty (i.e. they are now due at 5:00 p.m.).
However, we will not accept homeworks any later than that time, except
with previous arrangements.
You may collaborate with others on this entire homework.
However, please re-read the policy guidelines from
Handout #1.
Review Ch. 6.2, 6.3, and 6.4 of CLR for a review on probability, if
necessary. Read Ch. 8.3, 8.4, 10.2, and 13.4 of CLR.
Recall, these exercises are purely for your own practice. You need
only turn in the official problems.
- Do CLR 6.2-3
- Do CLR 6.2-4
- Do CLR 6.2-10, 6.2-11. (These are great problems!)
- Do CLR 8.2-5.
- Do CLR 11.3-4
- 1.
- Variant of CLR 6-2 (25 points).
The following program determines the maximum value in an unordered
array A[1..n].
Find-Max(A,n)
1 Randomly-Permute(A,n)
2 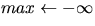 3 for
3 for 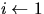 to n
4 do
to n
4 do  Compare A[i] to max.
5 if A[i] > max
6 then
Compare A[i] to max.
5 if A[i] > max
6 then ![$max \leftarrow A[i]$](img5.gif)
The call in line 1 re-orders the elements in the array by choosing a
uniformly random permutation of the items (see Extra Credit problem).
We want to determine the expected number of times the assignment in
line 6 is executed. Assume that all array entries are distinct.
- If a number x is randomly chosen from a set of i distinct
numbers, what is the probability that x is the largest number in the
set?
- When line 6 of the program is exectued, what is the
relationship between A[i] and A[j] for
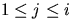 .
. - For each i in the range
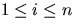 , what is the
probability that line 6 is exectued? Justify your answer.
, what is the
probability that line 6 is exectued? Justify your answer.
- Let
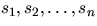 be n random variables, where
si represents the number of times ( or 1) that line 6 is
exectued during the ith iteration of the for loop. What is
E[si]?
be n random variables, where
si represents the number of times ( or 1) that line 6 is
exectued during the ith iteration of the for loop. What is
E[si]?
- Let
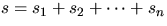 be the total number of times
that line 6 is exectued during some run of the program. Show that
be the total number of times
that line 6 is exectued during some run of the program. Show that
![$E[s] = \Theta(\lg n)$](img10.gif) .
.
- 2.
- (30 points)
In this problem, we give yet another proof that
randomized Quicksort runs in 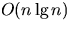 expected time. The
text gives a proof of this fact in Chapter 8.4, by giving a recurrence
relation which involves a summation over the possible partitions. In
lecture, we say a simpler argument based on labelling partitions as
``good'' or ``bad''. In this problem, we will get a tighter upper
bound on the expected number of comparisons which are performed, by
looking at the chance that any given two elements are directly
compared to each other.
expected time. The
text gives a proof of this fact in Chapter 8.4, by giving a recurrence
relation which involves a summation over the possible partitions. In
lecture, we say a simpler argument based on labelling partitions as
``good'' or ``bad''. In this problem, we will get a tighter upper
bound on the expected number of comparisons which are performed, by
looking at the chance that any given two elements are directly
compared to each other.
Input: 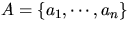 .
RQUICKSORT(A).
if |A| = 1, then return A.
else
Choose pivot element uniformly at random from A.
Compare pivot to all other elements. Let
.
RQUICKSORT(A).
if |A| = 1, then return A.
else
Choose pivot element uniformly at random from A.
Compare pivot to all other elements. Let
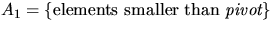
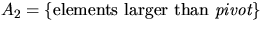 . return
. return 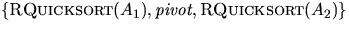 .end.
.end.
Assume that the sorted order of the elements is given by 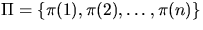 . For each possible pair of
unique elements i and j with
. For each possible pair of
unique elements i and j with 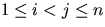 , we define a
0-1 random variable xij as follows:
, we define a
0-1 random variable xij as follows:
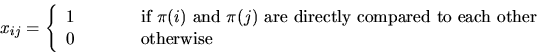
- Prove that
![$E[x_{ij}] = \frac{2}{j-i+1}$](img19.gif) . (Hint: To get
started, think about some special cases, such as the chance that
. (Hint: To get
started, think about some special cases, such as the chance that
 and
and 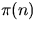 are compared, or
are compared, or 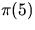 and
and 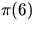 , or
, or
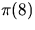 and
and 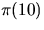 .
. - Let C be a random variable equal to the overall number of
comparisons performed during a single run of
Randomized-Quicksort. Give a simple formula for C in terms of the
various xij variables. Then use you formula, and the linearity
of expectations, to get an expression for E[C], using summations.
- Use your above expression to prove that
![$E[C] \leq 2nH_n$](img26.gif) , where
Hn is the Harmonic Number, defined on page 44.
, where
Hn is the Harmonic Number, defined on page 44.
- 3.
- Do CLR 11-3. (45 points)
You do not need to do part (d). You
should use the results as a given for other parts. Before starting
this problem, make sure you understand the multiple-array
representation of objects on p. 209.
Page 161 described a function Random(a,b), which returns an
integer between a and b inclusive, with each such integer being
equally likely. If programming in C, this would be similar to getting
the value 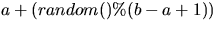 .
.
- Assume that Random is a constant-time function for
reasonable values of a and b. Give a
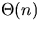 -time randomized
algorithm, which creates a uniformly random permutation of an array
A[1..n] of items.
-time randomized
algorithm, which creates a uniformly random permutation of an array
A[1..n] of items.
- Prove the correctness of your algorithm. Do not argue vaguely
that all outcomes are equally likely; instead, prove formally that the
probability of getting a particular permutation
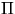 , is exactly
1/n!.
, is exactly
1/n!.
- Assume instead that your only source of randomness is a
constant-time function Random-bit, which returns either or
1 with equal probability. Argue that any algorithm which randomly
permutes the array requires
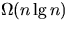 time.
time.
This document was generated using the
LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
3 for
to n 4 do
Compare A[i] to max. 5 if A[i] > max 6 then
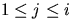 .
.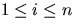 , what is the
probability that line 6 is exectued? Justify your answer.
, what is the
probability that line 6 is exectued? Justify your answer.
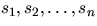 be n random variables, where
si represents the number of times ( or 1) that line 6 is
exectued during the ith iteration of the for loop. What is
E[si]?
be n random variables, where
si represents the number of times ( or 1) that line 6 is
exectued during the ith iteration of the for loop. What is
E[si]?
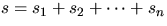 be the total number of times
that line 6 is exectued during some run of the program. Show that
be the total number of times
that line 6 is exectued during some run of the program. Show that
![$E[s] = \Theta(\lg n)$](img10.gif) .
.. RQUICKSORT(A). if |A| = 1, then return A. else Choose pivot element uniformly at random from A. Compare pivot to all other elements. Let
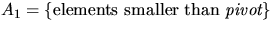
. return
.end.
![]() . For each possible pair of
unique elements i and j with
. For each possible pair of
unique elements i and j with ![]() , we define a
0-1 random variable xij as follows:
, we define a
0-1 random variable xij as follows:
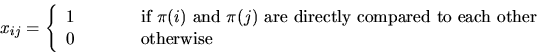
![$E[x_{ij}] = \frac{2}{j-i+1}$](img19.gif) . (Hint: To get
started, think about some special cases, such as the chance that
. (Hint: To get
started, think about some special cases, such as the chance that
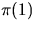 and
and 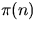 are compared, or
are compared, or 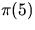 and
and 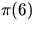 , or
, or
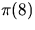 and
and 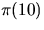 .
.![$E[C] \leq 2nH_n$](img26.gif) , where
Hn is the Harmonic Number, defined on page 44.
, where
Hn is the Harmonic Number, defined on page 44.