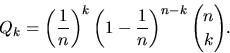Let
- Show that if
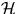 is 2-universal, then it is universal.
is 2-universal, then it is universal.
- Show that the class
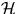 defined in Section 12.3.3 of CLR
is not 2-universal.
defined in Section 12.3.3 of CLR
is not 2-universal.
- Show that if we modify the definition of
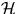 in Section
12.3.3 of CLR so that each function also contains a constant term b
also chosen uniformly at random from
in Section
12.3.3 of CLR so that each function also contains a constant term b
also chosen uniformly at random from 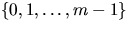 ,that is, if we replace h(x) with
,that is, if we replace h(x) with
then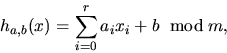
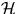 is 2-universal.
is 2-universal.
In class last week (and in Chapter 13.4 of the text), we saw that if you take a list of n items with distinct keys and insert them into a standard binary search tree using a random order, the expected height of the tree is
Assume that every object x has two associated values, key[x] and priority[x]. We define a new data structure called a treap, which is a binary tree with objects stored at internal nodes, satisfying the following two properties. (we assume that keys are distinct, and that priorities are distinct)
- If node y is the left (respectively right) child of node x, then key[y] < key[x] (respectively key[y] > key[x]).
- If node y is the child of node x, then priority[y] < priority[x].
- Assume that we have n objects, and that for each object x, we fix the value of key[x] and priority[x] in some way, so that all values are distinct. Prove that there must exist a unique treap containing those objects. (Hint: make sure that you prove both the existence and uniqueness.)
We would like to maintain a treap dynamically through a sequence of calls to Insert, Delete, and Search, as defined below. In the following three parts, we will ask you how to implement each of these operations while maintaining the properties of a valid treap. For each operation, you should briefly justify the correctness of your implementation as well as the bound on its running time. In describing your implementations, you may feel free to refer to descriptions of basic operations on binary trees as described in Chapter 13 of the text.
- Given an existing treap T, explain how to implement Search(T,k), which returns an object with key k if one exists in T. The running time of your operation should be O(height(T)).
- Given an existing treap T, explain how to implement Insert(T,x), where the values of key[x] and priority[x] are given as input. Your operation should result in a valid treap T' for the new set of objects, and the running time should be O(height(T)).
- Given an existing treap T, explain how to implement Delete(T,x), where you may assume that you are given a pointer to the location of object x in T. Your operation should result in a valid treap T' for the new set of objects, and the running time should be O(height(T)).
Up until now, we have assumed that an object given to Insert arrives with both a key and a priority. If we want to maintain a set of objects for which only the key is defined, we are free to choose any values we want for priorities, and the above routines will be correct. For the remainder of the problem, we assume that when an object x with key[x] is inserted, we set the priority of that object uniformly at random to a real number in the range [0,1]. (The probability that two different objects choose the identical priority is equivalently zero.)
- Assume that some sequence of operations has resulted in a treap containing exactly n objects. Argue that no matter what sequence of operations really took place, the current treap must look exactly like the standard binary tree which would have resulted if objects were inserted in order of decreasing priorities.
- Conclude that the expected running time of any given operation
is
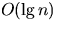 , where n is the number of objects in the data
structure before the operation begins.
, where n is the number of objects in the data
structure before the operation begins.