We wish to find the maximum of n numbers on a CRCW PRAM with p=n processors.
- Show that the problem of finding the maximum of
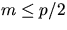 numbers can be reduced to the problem of finding the maximum of at
most m2/p numbers in O(1) time on a p-processor CRCW
PRAM. (Hint: Keep in mind that we know how to find the maximum
of k numbers in constant time with k2 processors. How can you
assign groups of processors to groups of input numbers to utilize this
fact?)
numbers can be reduced to the problem of finding the maximum of at
most m2/p numbers in O(1) time on a p-processor CRCW
PRAM. (Hint: Keep in mind that we know how to find the maximum
of k numbers in constant time with k2 processors. How can you
assign groups of processors to groups of input numbers to utilize this
fact?)
- If we start with
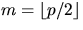 numbers, how many
numbers remain after k iterations of the algorithm in part (a).
numbers, how many
numbers remain after k iterations of the algorithm in part (a).
- Show that the problem of finding the maximum of n numbers can
be solved in
 time on a CRCW PRAM with p=n processors.
time on a CRCW PRAM with p=n processors.
Given an n-element list, where some elements of the list are marked as being blue, your goal is to create a list consisting of exactly the blue elements. Give an algorithm on an EREW PRAM, using P(n)=n processors, and
Show how to modify the Euler tour technique, to give EREW algorithms which compute the following information for an arbitrary n-node binary tree, using
- (6 points) The inorder numbering of all nodes
- (6 points) The preorder numbering of all nodes
- (6 points) The postorder numbering of all nodes
- (12 points) The size of the subtree rooted at each node
( Hint: Take the difference of two values in a running sum along an Euler tour. Alternatively, since you already know how to compute the answers to parts a, b, and c, can you use this information?)