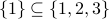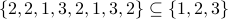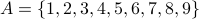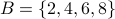CSCI-1080 Intro To CS: World Wide Web
Saint Louis University, Department of Computer Science
Set Theory
Sets
A set is a collection of objects. These objects are called the elements or members of the set. Objects can be anything: numbers, people, other sets, etc. Objects can be anything: numbers, people, words, Web sites, other sets, etc.
If 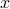 is a member of
is a member of 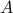 , then we write
, then we write 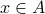 . We may also say that x “belongs to” A, or that x “is in” A.
. We may also say that x “belongs to” A, or that x “is in” A.
If 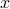 is not a member of
is not a member of 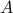 , then we write
, then we write 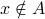 .
.
Examples of sets include:
movies on Netflix
Students enrolled in this class
Computers on the Internet
single-digit positive integers
integers that are not divisible by 6
We often use variable names to refer to sets and objects. Usually, upper-case letters refer to sets and lower-case letters refer to objects. If 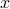 is an element of set
is an element of set 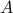 , then we write
, then we write 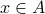 . If
. If 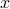 is not a member of
is not a member of 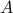 , then we write
, then we write 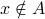 .
.
A set is completely defined by its elements. This implies two key properties of sets:
Order of elements in a set is irrelevant. There is no distinction of “first element” or “second element” etc.
Repetition of elements in a set is irrelevant. For example, no matter how many times 3 is named as a single-digit positive integer, the set of single-digit positive integers does not change.
Two sets A and B are defined to be equal when they have exactly the same elements: every element of A is an element of B and every element of B is an element of A. In this case, we write A = B. We also allow for an empty set, which is the set with no elements.
Explicit and Implicit Set Notation
Explicit Notation for Sets
The simplest way to describe a set is to list its elements inside a pair of curly braces. This is known as explicit set notation.
For example:
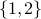 denotes the set whose only elements are 1 and 2.
denotes the set whose only elements are 1 and 2.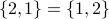
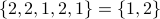
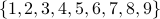 denotes the set of single-digit positive integers.
denotes the set of single-digit positive integers.
The simplest possible example of explicit set notation is 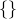 , which denotes the empty set.
, which denotes the empty set.
Cardinality
The cardinality of a set 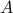 is the number of elements in
is the number of elements in 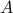 , which is written as
, which is written as 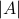 . Note that this vertical bar notation looks the same as absolute value notation, but the meaning of cardinality is different from absolute value. In particular, absolute value operates on numbers (e.g.,
. Note that this vertical bar notation looks the same as absolute value notation, but the meaning of cardinality is different from absolute value. In particular, absolute value operates on numbers (e.g., 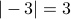 ) while cardinality operates on sets (e.g.,
) while cardinality operates on sets (e.g., 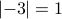 ).
).
Examples of cardinality:
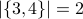
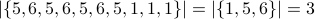
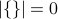 . The empty set has no elements.
. The empty set has no elements.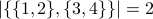 . In this case the two elements of
. In this case the two elements of 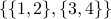 are themselves sets:
are themselves sets: 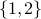 and
and 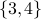 .
.
We can also consider the cardinality of infinite sets, a topic made cool by Georg Cantor. His work is beyond the scope of this introduction.
Subsets
Given two sets 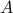 and
and 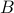 , we say that
, we say that 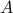 is a subset of
is a subset of 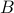 if every element of
if every element of 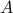 is also an element of
is also an element of 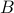 . We write
. We write 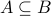 to denote that
to denote that 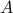 is a subset of
is a subset of 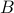 .
.
For example:
Let 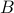 be the set of registered students at SLU, and
be the set of registered students at SLU, and 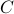 be the set of registered students in this class. Then
be the set of registered students in this class. Then 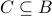 .
Think about why it is true that
.
Think about why it is true that 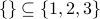 . There is a somewhat subtle mathematical principle at work in this statement. That same principle is invoked by this statement: “I am friends with every 100-feet-tall person who has ever lived.”
. There is a somewhat subtle mathematical principle at work in this statement. That same principle is invoked by this statement: “I am friends with every 100-feet-tall person who has ever lived.”
Venn Diagrams
A Venn diagram is an illustration that represents one or more sets and the relationships between them. For example, suppose 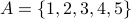 and
and 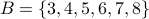 . Below is a Venn diagram of
. Below is a Venn diagram of 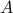 and
and 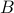 :
:
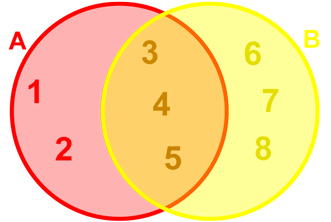 |
Venn diagram
Usually, Venn diagrams are drawn more simply, without listing the elements of the sets:
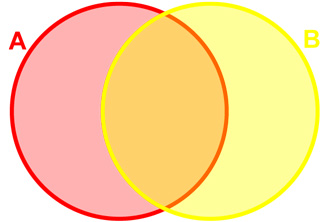 |
Typical Venn diagram representation |
With different examples of sets, the Venn diagram will look different. The circles might not overlap at all, or one circle might be completely contained inside another.
Union and Intersection The union of two sets A and B is the set consisting of any object that is (1) an element of A, or (2) an element of B, or (3) an element of both A and B. The union of A and B is written as A ∪ B.
Examples:
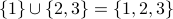
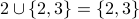
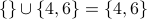
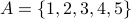 .
. 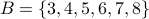 .
. 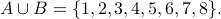
The intersection of 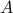 and
and 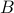 is the set of all objects that are elements of both
is the set of all objects that are elements of both 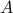 and
and 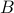 . The intersection of
. The intersection of 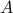 and
and 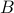 is written as
is written as  .
.
Examples:
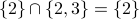
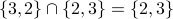
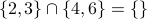
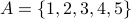 .
. 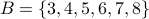 .
. 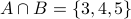 .
.
The above examples involving sets 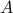 and
and 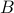 can be drawn as the following Venn diagram:
can be drawn as the following Venn diagram:
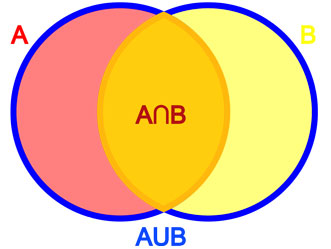 |
Venn diagram of union and intersection |
Ordered Lists
If we consider “the songs on my iTunes” as a familiar example of a set, then “a playlist on my iPhone” is the corresponding example of an ordered list. Key properties of ordered lists include:
Order of elements in an ordered list is relevant.
Repetition of elements in an ordered list is relevant.
Explicit notion for writing ordered lists is similar to that for sets; however, we use parentheses instead of curly braces. For example:
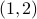 is an ordered list that is different than
is an ordered list that is different than 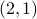
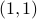 is an ordered list that is different than
is an ordered list that is different than 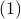
From now on, expressions with parentheses “( , , , )” and expressions with curly braces “{ , , , }” have very distinct meanings!
The length of an ordered list is, intuitively speaking, just like the number of songs in a playlist. For example:
The length of
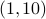 is
is 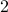
The length of
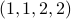 is
is 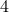
An ordered pair is an ordered list of length two. We will use ordered pairs very often in our study of the Web; we will use longer ordered lists less often. Also, we will never attempt to define the cardinality of an ordered list. Sets have cardinality. Ordered lists have length.
Any element in an ordered list can itself be an ordered list or a set. Any object in a set can be a set or an ordered list. For example:
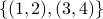 is a set of two elements, each of which is an ordered pair. One of the elements of the set is
is a set of two elements, each of which is an ordered pair. One of the elements of the set is 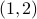 and the other element of the set is
and the other element of the set is 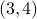 .
.
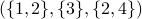 is an ordered list of sets. The first element of the list is the set
is an ordered list of sets. The first element of the list is the set 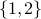 ; the second element of the list is the set
; the second element of the list is the set 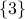 ; the third element of the list is the set
; the third element of the list is the set 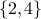 .
.
Implicit Notation for Sets
Explicit set notation is convenient for small sets but impractical for large sets, such as the set of all Web pages. Implicit set notation (also called set builder notation) is a more sophisticated way to describe sets with mathematical rigor.
There are two parts to any implicit set expression:
A dummy variable. Very often we will use x as our dummy variable. A logical true/false statement. Usually, this statement is an expression that uses the dummy variable. These two parts are enclosed within curly braces and separated by a colon (“:”). For example:
A = {x : x is a single-digit positive integer}
B = {x : x is an even element of set A}
The above two sets can also be written explicitly:
How to interpret implicit set notation
Suppose P(x) is any logical true/false statement that uses x in some way. (For example, P(x) = “x is a single-digit positive integer”; or P(x) = “x is a Web page”.) With that, we can write implicit set notation that looks like this: 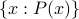 . The set defined by
. The set defined by 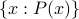 is the set of all objects for which logical statement P is true. For example:
is the set of all objects for which logical statement P is true. For example:
Suppose P(x) = “x is a Web page”; then
{x: P(x)} = {x: x is a Web page}
http://www.slu.edu/index.html
 {x: x is a Web page}
{x: x is a Web page}Flavio Esposito
 {x: x is a Web page}
{x: x is a Web page}|{x: x is a Web page}| is approximately 50 billion
Statement #3 above is true because “http://www.slu.edu/index.html is a Web page” is true. Similarly, statement #4 above is true because “Flavio Esposito is a Web page” is false.
Logical Expressions
Grossly simplifying an entire branch of mathematics (logic) to suit our Web-focused ends, we note three kinds of logical true/false statements, often referred to as expressions:
Constant expressions such as “True” and “False” are the simplest possible logical true/false statements, each with meaning that is evident. The truth or falsehood of a constant expression is always the same; it does not depend on the value of any dummy variable.
Simple expressions are like simple clauses in English, which have one verb. Usually they involve a dummy variable. For example:
x = 3 is a simple true/false expression. Its truth or falsehood depends on x.
Suppose A is the set of all Web pages. Then “
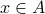 ” is a simple true/false expression.
” is a simple true/false expression.Suppose N is a number with a specific value (e.g., 3). Then “
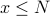 ” is a simple true/false expression.
” is a simple true/false expression.As illustrated above, possible “verbs” in mathematical true/false expressions include the following: “=”, “
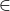 ”, and “
”, and “ ”.
”.
Compound expressions are like compound sentences in English. They combine expressions (simple or compound) with conjunctions like “and” and “or”. For example:
x is an integer and
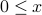 and
and 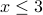
x is a contact on my iPhone or x is a song I heard on the radio this year
x is a Web page with a hyperlink pointing to http:www.slu.edu/ and x is not authored by Flavio Esposito
Compound expressions with “or”
Suppose we have two true/false statements: P, Q. We can use the mathematical conjunction “or” to combine these into a single compound expression “P or Q”. The truth or falsehood of “P or Q” is defined as follows:
Mathematical definition of “or” as illustrated by “P or Q”
P is True, Q is True
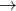 “P or Q” is True
“P or Q” is True P is True, Q is False
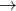 “P or Q” is True
“P or Q” is TrueP is False, Q is True
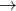 “P or Q” is True
“P or Q” is True P is False, Q is False
 “P or Q” is False
“P or Q” is False
Compound expressions with “and”
Suppose we have two true/false statements: P, Q. We can use the mathematical conjunction “and” to combine these into a single compound expression “P and Q”. The truth or falsehood of “P and Q” is defined as follows:
Mathematical definition of “and” as illustrated by “P and Q”
P is True, Q is True
 “P and Q” is True
“P and Q” is True P is True, Q is False
 “P and Q” is False
“P and Q” is FalseP is False, Q is True
 “P and Q” is False
“P and Q” is FalseP is False, Q is False
 “P and Q” is False
“P and Q” is False
Union and intersection defined formally
Using implicit set notation and compound logical expressions, we can restate the definitions of union and intersection more formally than we did when we introduced the terms.
For any two sets A and B:
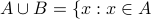 or
or 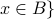
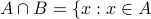 and
and 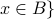
The above definitions mathematically restate the familiar Venn diagram:
 |
Similarity of Sets
We measure the similarity of two non-empty sets A and B with the Jaccard Index:
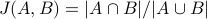 .
.
If A and B are disjoint then J(A,B)=0. If A=B then J(A,B)=1. (Assuming A and B are non-empty.)
Suppose 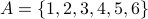 . Below we use J(A,B) to measure the similarity of set A with 5 different example sets B:
. Below we use J(A,B) to measure the similarity of set A with 5 different example sets B:
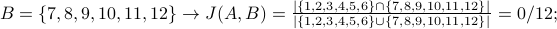 (not similar at all)
(not similar at all)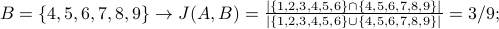 (somewhat similar)
(somewhat similar)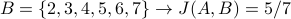 (quite similar)
(quite similar)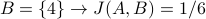
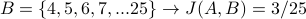
The contect of this site is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.